Break-even is broken

This article was published in 2016.
Why the use of the break-even cut-off grade is flawed, and how it poses a fundamental problem for the mining industry
Sometimes what we are taught is not right anymore (if it ever was)
The lead author’s father was taught at school that the ‘nucleus of an atom was the smallest indivisible piece of matter’. It was then an undisputable truth. We now know of course about quarks, muons and neutrinos. In this article, we invite the reader to reconsider what they were taught on how break-even grades should be calculated and used, and how cut-off grades are selected for use in mining studies and ore reserves estimation.
The authors contend that the way the base and precious metals mining industry uses break-even grades is not consistent with the stated objectives of the mining company, and therefore if not plainly wrong, is at least deeply flawed and subject to so many sources of error that value is almost guaranteed to be destroyed.
Like using Newtonian physics in a quantum physics world, we contend that the way that the majority of the mining industry calculates ore reserves with a break-even equation is no longer appropriate – it is broken. In addition, it is a major contributor to the underlying problems with the financial returns of the mining industry. As will be shown in the case study in this article, an error of just 0.1 g/t in the break-even cut-off grade of a large-scale open pit gold mine can result in 50-60 per cent of the ore reserve having zero value. The authors contend that it is more common than not that mines have ore reserves with this scale of error.
While the current process that is commonly used to estimate an ore reserve is deeply flawed, the resulting declared ore reserve is not necessarily invalid. The JORC Code only requires that the ore reserve is shown to be ‘economically mineable’ (JORC, 2012) and does not say anything about an ore reserve having to exclude substantial tonnages that are negative in value and will lose money. However, it is implied in the JORC Code that the ore reserves quoted are what will be mined and processed by the mining company.
The purpose of a cut-off grade
Mining companies will generally state their goals, purpose or mission to be something similar to:
- ‘create long-term shareholder value’ (BHP Billiton, 2015)
- ‘deliver strong and sustainable shareholder returns’ (Rio Tinto, 2015)
- ‘deliver superior returns’ (Newcrest, 2015).
This can only be achieved by a selected combination of share price growth and dividends.
Given that the cut-off grade is the key decision variable determining what is processed in a mine (and what is not, with ore processing being the main value-generating function of a mining company), the purpose of the cut-off grade should be to enable the mining company to achieve its previously stated overall goals (ie creating shareholder value from the mine in which the cut-off grade is being applied). If the cut-off grade is not doing this, the company cannot achieve its stated aims.
The break-even grade
The cut-off grade used by most mining companies for the ‘process/do not process’ decision, rightly or wrongly, is the break-even cut-off grade.
The break-even grade is defined as the grade at which revenue obtained is equal to the cost of producing that revenue. The simple break-even formula to determine this is:

Although the formula is simple, many companies spend a lot of time and energy arguing over what costs shouldbe included.
In addition, what is commonly not recognised, or is dismissed as not being particularly important, is the fact that the recovery is usually a function of grade and that both the cost and payability can also be a function of grade.
So, in fact, the simple formula is not so simple after all.
It is also important to note that this definition of the cut-off grade being used for the estimation of ore reserves and the planning of the mine (the break-even cut-off grade) is not the same as the stated objective of the mining company – to deliver shareholder value. Thus, the use of a break-even cut-off grade will lead to mine plans that are almost guaranteed to not deliver the company’s stated goals.
This then begs the question: why are companies using a break-even cut-off grade? The authors suggest that they are simply oblivious to the effects of what they are doing.
The marginal tonnage issue in ore reserves
Although it is not often appreciated, a key feature of many stated ore reserves estimates is that a significant portion of the ore reserves tonnage is marginal in value.
While this is well-known and understood by mining engineers heavily involved in the preparation of ore reserve estimates and strategic long-term planning, it has become apparent to the authors that the vast majority of mining executives do not understand how marginal much of their companies’ ore reserves actually are. This is especially the case for executives from a non-technical background.
Figure 1 presents an example of the distribution of an ore reserve tonnage by value for an actual open pit copper-gold mine (Mine A). The distribution shown is typical of many orebodies when a break-even cut-off value (grade) is used to estimate the ore reserves. A significant portion of the ore reserve tonnage is of low or marginal value.
The distribution of total value for this ore reserves estimate is shown in Figure 2. The grades of the material have been converted to equivalent net values expressed in dollars per tonne.
In this particular distribution, an interesting symmetry was present. The bottom 27 per cent of the ore reserve by tonnage held 6 per cent of the value, while the top 27 per cent held 60 per cent of the value, equating to ten times the value for the same tonnage. In effect, a lot of the ore reserve was being mined and processed for little more than ‘practice’.
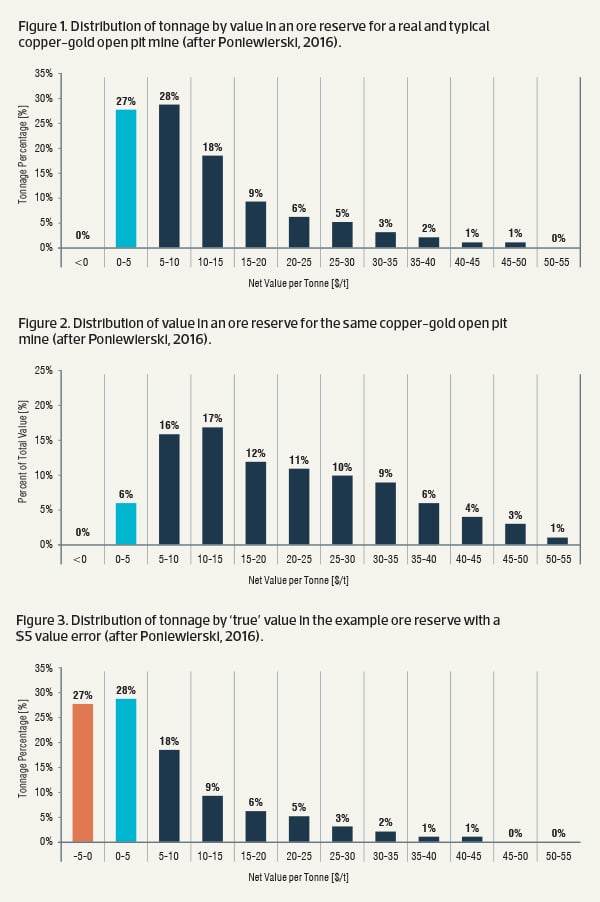
The effect of small errors in the break-even cut-off grade on ore reserve value
Using the cut-off value/tonnage distribution for Mine A, it can be seen that a marginal break-even cut-off grade for the ore reserves estimate can have a significant downside effect if there is an error in calculating the break-even cut-off grade. Such an error would result in a significant portion of the stated ore reserves becoming negative in value.
If the error was equivalent to $5/t in value (be it a cost or revenue error or a combination of both), the distribution shown in Figure 1 would be modified to the value distribution shown in Figure 3. In total, 27 per cent of the ore reserve tonnage would then be in the -$5/t to $0/t value bin and a similar tonnage would be in the $0/t to +$5/t value bin. As a result, a total of 55 per cent of the ore reserve would effectively have zero value.
The $0/t to +$5/t value bin tonnes should be contributing to the capital payback of the project and adding to the value of the total project. Instead, they are ‘supporting’ the loss associated with the -$5/t to $0/t value bin tonnage.
To understand how easy it is to have a $5/t error in the cut-off grade, at a gold price of A$1640/oz (current at the time of writing), a $5/t error is induced by any error that changes the calculated cut-off grade by 0.095 g/t (which the authors have rounded up to 0.1 g/t).
So an error of 0.1 g/t in the break-even cut-off grade calculation of a large-scale, low-grade open pit gold mine (for which the previously discussed value distribution is typical) will result in 50-60 per cent of the ore reserve having zero value. This is quite disturbing to realise and is generally unappreciated within the industry.
The authors refer to these ore reserves as ‘negative geared’. Negative geared ore reserves are discussed in more detail in a paper written by Poniewierski (2016) for the Project Evaluation 2016 conference.
The two most common errors
The two most common errors that the authors have seen in the calculation of break-even cut-off grades, which lead to negative geared ore reserves, are:
- the fixed recovery error
- the omission of sustaining capital costs.
The fixed recovery error refers to the use of a constant fixed recovery percentage for all head grades down to the break-even grade. For example, consider a mine with a gold head grade of 2.2 g/t that has been evaluated to have a recovery of 94 per cent at the 2.2 g/t head grade. If the 94 per cent recovery value is used to determine a break-even grade, it would be 0.4 g/t, which implies a tails grade of 0.02 g/t. This is a tails grade so low that, to the authors’ knowledge, no operating gold mine has ever achieved it. At a head grade of 2.2 g/t, a recovery of 94 per cent implies a tails grade of 0.13 g/t.
If it is recognised that the recovery varies with head grade and a fixed tails grade is used to assess the recovery instead of a fixed percentage recovery, the same cost and price conditions that resulted in a break-even cut-off grade of 0.4 g/t for the fixed percentage recovery would result in a break-even cut-off grade of 0.5 g/t. This is a difference of 0.1 g/t, which is sufficient to make 50-60 per cent of the ore reserve previously calculated with the fixed percentage recovery of zero value.
An examination of JORC Table 1 releases shows that the fixed recovery approach is being used to determine the break-even cut-off grade of a large percentage of ore reserves.
The second item, the omission of sustaining capital costs, can result in a significant underestimation of the true costs and therefore a significant underestimation of the break-even cut-off grade.
Hall (2014) discusses the sustaining capital in detail. Sustaining capital is expenditure that maintains existing capabilities as opposed to ‘project capital’ that is used to buy capability (or capacity).
For maintaining existing capital items, there is no conceptual difference between replacing an oil filter every 50 hours (an operating cost) and replacing a truck engine every 16 000 hours (a capital cost) or a truck every 50 000 hours (a capital cost). Therefore, sustaining capital is conceptually a ‘lumpy’ irregular expense that is classified by accountants as capital rather than operating costs purely by virtue of the spending pattern, not the underlying nature of the cost. By capitalising these irregular expenses, accountants are able to use depreciation to more evenly spread these ‘lumpy’ costs out over the useful life of the equipment being maintained. As such, sustaining capital needs to be included in the cut-off grade calculation.
Some examples of sustaining capital costs that should be included are discussed in Poniewierski (2016) and Hall (2014).
How should break-even be calculated?
The authors contend that the only true method of evaluating a correct break-even cut-off grade is to undertake a set of scenarios with varying cut-off grades and production rates. If these scenarios are evaluated in a financial model that accurately reflects the costs of each scenario and the undiscounted cash flows are graphed as shown in Figure 4 (where, in this case, the y-axis of ‘increasing value’ is the project total undiscounted cash flow), the cut-off grade that results in the largest undiscounted cash flow is the true break-even cut-off grade.
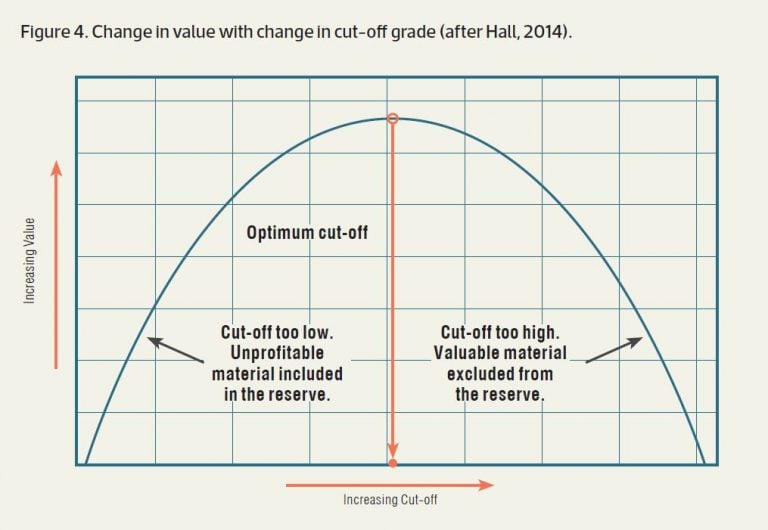
By definition, a cut-off grade less than the identified peak cash flow cut-off grade and that results in a lower total cash flow must include material that is losing value.
Should we be using break-even at all?
The authors also contend that we should not be using the break-even grade at all. If the time value of money is recognised, a cut-off grade higher than the calculated break-even grade will usually be one that maximises net present value (NPV) (for a fixed selected cut-off grade value), as discussed in Hall and de Vries (2003) and Hall (2014). In this case, for the y-axis shown in Figure 4, the ‘increasing value’ is the project total NPV (discounted cash flows).
Further refinement is possible, resulting in a cut-off grade policy of varying cut-off grades over the life-of-mine that will increase the NPV, as discussed by Lane (1997), Whittle (2015) and King (2001).
Sub-grading
The authors recognise that there is a perception in the mining industry that increasing the cut-off grade above the currently used and publicised break-even cut-off grade leads to accusations of ‘high grading’. The term generally has a negative connotation and is always an accusation that the mined grade is higher than it should be; picking the eyes out of the resource, sterilising ore and thereby destroying value.
If that’s what increasing the cut-off grade is really doing, then it is indeed a bad thing. But this begs the question of what the grade ‘should be’! Presumably, it should be the grade that delivers on the company’s goals – providing shareholder returns and value.
Over the course of numerous strategy optimisation studies, the authors have never found an operation high grading above the grade that maximises cash generation. However, many are ‘sub-grading’, which involves mining and treating grades that are substantially lower than the cash maximisation grade and using higher-grade ores to subsidise loss-making ore tonnages.
The authors suggest that mining with a properly engineered mine plan at the grade that delivers the company’s goals is ‘right grading’. Typical plans are therefore sub-grading, which should be just as pejorative a term as high grading. To a sub-grader, right grading will look like high grading. But what right grading has eliminated from the sub-grader’s mine plan is material that is actually destroying value, which should not have been in the plan in the first place. Sterilising value-adding material is not destroying value, which is the feared outcome of high grading.
Mining is a business, and a business does no one any favours by setting itself up for failure.
Conclusion
The use of the break-even cut-off grade is a fundamental problem that is exacerbating the poor financial returns of the mining industry. We leave the reader with a final thought that should be the new mantra on cut-off grades:
‘Cut-off grade should be an outcome of a mining study that has been undertaken to meet the company’s stated value goals. Cut-off grade should not be a predefined input into such a study, as this will guarantee that the company’s value goals will not be met.’
References
BHP Billiton, 2015. Resourcing Global Growth: Annual Report 2015.
Hall B, 2014. Cut-off Grades and Optimising the Strategic Mine Plan, Spectrum Series 20, 311 p (The Australasian Institute of Mining and Metallurgy: Melbourne).
Hall B E and de Vries J C, 2003. Quantifying the economic risk of suboptimal mine plans and strategies, in Proceedings Mining Risk Management Conference 2003, pp 191–200 (The Australasian Institute of Mining and Metallurgy: Melbourne).
JORC, 2012. Australasian Code for Reporting of Exploration Results, Mineral Resources and Ore Reserves (The JORC Code) [online]. Available from: <www.jorc.org> (The Joint Ore Reserves Committee of The Australasian Institute of Mining and Metallurgy, Australian Institute of Geoscientists and Minerals Council of Australia).
King B, 2001. Optimal mine scheduling, in Mineral Resource and Ore Reserve Estimation – The AusIMM Guide to Good Practice (ed: A C Edwards), pp 451–458 (The Australasian Institute of Mining and Metallurgy: Melbourne).
Lane K F, 1997. The Economic Definition of Ore, second edition (Mining Journal Books: London).
Newcrest, 2015. Our values [online]. Available from: <www.newcrest.com.au/careers/work-with-newcrest/careers-our-values> [Accessed: 19 March 2015].
Poniewierski J, 2016. Negatively geared ore reserves – a major peril of the break-even cut-off grade, in Proceedings Project Evaluation 2016, pp 236–247 (The Australasian Institute of Mining and Metallurgy: Melbourne).
Rio Tinto, 2015. About Rio Tinto [online]. Available from: <www.riotinto.com/aboutus/about-rio-tinto-5004.aspx> [Accessed: 19 March 2015].
Whittle G, 2015. Whittle Optimisation – the money mining methodology and its impact on ore reserves,
in Mineral Resource and Ore Reserve Estimation –
The AusIMM Guide to Good Practice, second edition, Monograph 30, pp 525 – 528 (The Australasian Institute of Mining and Metallurgy: Melbourne).